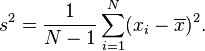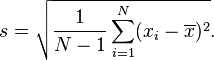What are the Mean and Standard Deviation
Whenever you look at something, make a measurement, consider a qualification, or make a judgment; you’re probably wrong.
Now now, don’t take it personally. You’re probably not THAT wrong. But you almost certainly didn’t actually get it exactly right. In fact, apparently on a fundamental level there’s often no such thing as being exactly right, so you can take comfort in the fact that you’re only just kind of probably existing in any particular way right now. Or be horrified. One of those things that people do.
But, knowing that we’re probably wrong about everything doesn’t mean that we can’t get useful information. In fact, it means we can get EVEN MORE information. Because now that we know we’re wrong, we can figure out How Wrong We Are.
That’s what Standard Deviation is for.
But in order to know how wrong we are, we first have to try to be right despite being wrong. Which is easier than it sounds. Basically you just keep trying again and again and again, until you’ve done it enough times that the right answer is PROBABLY in there somewhere. Or something close to it anyway, in case the right answer doesn’t actually exist.
Once we’ve done all that, we can figure HEY, we were trying to get the right answer every time. So we can probably figure every measurement we made was somewhere around there. Where is THERE.
That’s the Mean(or more relatably, the Average) is for.
—
Now, the mean can be pretty useful. It’s one very specific measurement that you can point at and say “HAH! There it is! That’s the answer!” Which is good when you need to be able to do that sort of thing. But it doesn’t really reflect all that effort we went through to obtain it, or give us any idea how likely it is that we’re actually right about what that answer is.
In fact, I could be really sneaky, and just take one measurement. Then my mean is my measurement, bam, done. TIME SAVING. YAY!
But what if you were actually wrong? Let’s say you make one measurement, it’s two. BAM, TWO. FINAL ANSWER. Only … if you were to make another measurement it would be 6. Whoops. You were way off. So you make another, and it’s 3. Maybe you weren’t so off! Then you make another, and it’s 5. Then you just get sick of it and decide to go with something.
So your numbers are 2; 3; 5; 6. You know what? Close enough. But you still have to be able to tell someone the answer. So you go ahead and take the average(Mean).
To do that, you add up all your measurements, and divide that by the number of measurements you took.
So 2+3+5+6 = 16, and you took 4 measurements. 16 divided by 4 is 4. So there you go! Four! That’s your answer. Print it up, send it off, science is exhausting, time to take a nap.
—
But wait, that isn’t really telling the whole story now is it. And just telling someone “4” doesn’t even go into all that exhaustive effort you did taking all those wrong measurements to get to it, let alone give an accurate picture of what they could likely expect if they decided to see the answer for themselves. They might be even lazier than you, pull up 6, and decry you for a scoundrel and a liar! Then you wind up with an angry mob outside your laboratory, torches and pitchforks at the ready, screaming obscenities and accusations of Mad Science. This is usually considered an outcome that is best avoided.
So ok, maybe it’s best if you admit how wrong you are before someone else finds out … but how wrong ARE you, really? How can you tell! You could just look at the numbers for awhile and guess I suppose, but then you’re just adding another measurement(your guess), and your guess isn’t likely to change just by looking at it, so if you wanted to pull up more guesses, you’d have to get more people, and then you’d have to average them, and then you’d have to figure out how wrong THOSE guesses were, and …… yeah, that could get complicated.
So, let’s use our trusty friend, math! Apparently the standard deviation is meant for that sort of thing, so let’s see what that looks like.
Wait! No! Don’t run away! It’s actually not that bad!
What it’s really saying is,
1. Figure out the average of all your measurements.(x̄ )
2. Look at all your measurements, figure out how far off they are from the average. That’s your error. Now square it(multiply it by itself), so we don’t have to worry about it being negative.(xi – x̄)^2
3. Add all your squared errors from 2 together. (the funny sigma symbol, with N on top and i=1 at the bottom, basically, “sum(add up) everything inside from when i is 1 to N”)
4. Divide it by one less than the number of measurements you have. (N-1)
5. Square root your answer from step 4, because squared errors actually make things look worse or better than they really are in the mostly arbitrary fashion of how far they are from one.
And … there you go! MAGIC! Ok, it still looks pretty complicated, but still not as bad as it looks.
Our numbers from before were 2; 3; 5; 6. So how do we get our standard deviation(s) from them?
Well, we figured out our mean earlier, before the angry mob came because they got the wrong answers too. It was 4.
So, we figure out the error for all our numbers
2-4 is -2, but we’re squaring it, and (-2)*(-2) is 4
3-4 is -1, and squaring it just leaves us with 1
5-4 is 1, again, just 1
6-4 is 2, so we get 4 again.
4+1+1+4 is 10, but we took four measurements, so we get to split the load of that error among them.
So we divide by one less than the number of measurements we took. There’s a pretty decent reason for that that I might explain next week, but for now, consider it just punishment for having a sample size small enough where subtracting one from it actually bothers you.
10 / (4-1) is 10/3, which is 3 and a third. Better, though still kind of high.
But ah, we squared everything, so now we get to square root it too. We could square root it by figuring out the square root of 10 and dividing it by the square root of 3. Or just dividing 10 by 3 and square rooting what comes out. I don’t know about you, but I have no idea what either of those numbers are, so I’m just going to use a calculator. The number comes out to (decimal)1.825741858350553711523232609336, which is ridiculous(And also explains why we didn’t know it offhand.) And now we’re done. Bam, S calculated, time to take a nap.
—–
Oh wait, but guess what. Our measurements weren’t actually that precise. They were all just plain whole numbers that obviously weren’t very accurate to begin with. That means most of that gigantic number we can actually just throw out, because it’s based on data we never actually measured. Now, if our answers were all something like 2.0000000000000000000000 that might be a different story, and every one of those digits would actually be relevant. But then we probably wouldn’t have gotten to experience the magic of getting such wildly different responses, or we would probably have to start seriously questioning our methods
Now, there’s a whole complicated set of rules for deciding just how much of the numbers we’ve calculated based on our measurements we get to keep in the end, and maybe I’ll get into those another time, but basically, we did a bunch of multiplication and division, which means we get to keep the same number of numbers(significant digits) we started with. That is, one number. We round the next digit up or down(depending on whether it’s less than 5 or not), it was 1.8, so picking the number it’s closer to(1 or 2), we come up with … 2.
Therefore, we can report our data, which in this case was 2; 3; 5; 6, as being 4, plus or minus 2.
—–
Which is a pretty fantastic result really. The center was 4, 4-2 is 2(our minimum), 4+2 is 6(our maximum). 4 +/- 2 actually represents our data perfectly, without even having to give up any of our observations. We might have even been able to figure out both those numbers just by looking at it, but that isn’t always such an option.
The real power is we can use all this for any set of data that’s SUPPOSED TO be the same, take all our measurements, average them, figure out how spread out all our data is, and then take all that and report two relatively simple numbers that accurately describe both our result and how close we likely came to it.
We could even graph it.
Now, it’s not always quite that neat and pretty. Sometimes our measurements might be really tightly contained, and obviously close to the accurate result, but then have one that shoots way off out into nowhere for no apparent reason. These outliers are usually worth studying on their own to figure out just why that happened, if only to notice a mistake you made with the measurement, and they should never be removed. Altering data is about the worst thing you could do in science, and totally justifies the pitchfork and torches treatment. If you see a graph of actual data points that don’t have some points that simply don’t quite fit right, you should be extremely suspicious.
But they also obviously shouldn’t SEVERELY affect your data’s overall tendency. And as long as you have enough data, by calculating the standard deviation, they don’t. Because all your errors get divided out and distributed amongst all your measurements, that huge error becomes a lot less huge when you have, say, 1000 points all maintaining a tighter cluster with much lower error. It still pushes your data slightly further out, which it should, because this is the accuracy of your experiment we’re talking about, but all the rest of your data still keeps its usefulness.
Of course, when you have 1000 data points, doing all this manually would be a considerable pain, whether or not you understand it completely. Which is why just about any complex enough calculator will have statistical programs built in for analyzing lists, and there are plenty of online and software tools you can use if you don’t have one. Including spreadsheet programs such as Excel and Openoffice Calc. In Calc, =STDEV(*select your dataset*), and =AVERAGE(*select your dataset*), will give you your answers quick and easy, whether you’ve got 4 cells of data or 4000.
—-
Here’s a rather nice stat calculator for android – Stat Calculator by the coffee drinker
– The Arithmetic mean is what we’ve been working with, and you have to scroll down on the statistic section for the standard deviation. Also, the variance at the very bottom is what you get before you square root it for the standard deviation(seen above as s^2).